SDOI2015 Round1 Solution[完结]

dzy posted @ 2015年4月13日 10:07 in 专题 , 3679 阅读

作为一只不在SD省的蒟蒻，很有幸膜拜到了贵省的题目。

我就稍微讲讲做法吧。（其实还有代码反正都是为了骗访问量>_<）

 

D1T1 排序[OK]  D1T2 寻宝游戏[OK]  D1T3 序列统计[OK]

D2T1 星际战争[OK]  D2T2 约数个数和[OK]  D2T3 道路修建[OK]

 

终于推完了。。不过因为还没有得到数据，并不敢保证代码一定能AC。。。

[UPD 4.15]BZOJ上有数据了。好像都A了。

 

【D1T1 排序】

我们考虑已经使用了$1\sim i-1$这些操作中的某些操作后，判断能否继续排序以及是否需要第$i$次操作。

我们把序列分成$2^{n-i}$块，这样每段的长度都是$2^i$。我们定义一段是合法的，当且仅当这段数是从小到大排列的而且是连续的。如果发现有超过2段是不合法的，那这个序列显然就没救了，因为一次操作只能改变两段的状态。

如果一段是不合法的，那把它从中间剖开，形成的两段应该都是合法的，只有一种交换方法，判断是否可行。

假设有2段不合法，都从中间剖开，就得到了4段合法的序列。有4种交换方法，枚举是否可行即可。

因为操作的顺序是没有影响的，所以用了几次操作，最后答案就加上操作数量的阶乘即可。

这样我们就得到了一个搜索的程序，感觉合法的状态并没有很多，好像可以跑出极限数据，然而我并不清楚复杂度。


#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
int n, bad;
vector<int> a;
typedef long long ll;
ll fact[15], ans;
void flip(vector<int> &A, int x, int y, int len){
	for(int i = 0;i < len;i ++)
		swap(A[x + i], A[y + i]);
}
int check(vector<int> A, int x, int y){
	for(int i = x + 1;i <= y;i ++)
		if(A[i] != A[i - 1] + 1) return 0;
	return 1;
}
void dfs(vector<int> A, int i, int cnt){
	if(i == n){
		ans += fact[cnt];
		return;
	}
	int b[5], tot = 0;
	for(int j = 0;j < (1 << n);j += (1 << (i + 1))){
		if(!check(A, j, j + (1 << (i + 1)) - 1)){
			if(tot == 4) return;
			b[++ tot] = j, b[++ tot] = j + (1 << i);
		}
	}
	vector<int> B;
	if(!tot) dfs(A, i + 1, cnt);
	if(tot == 2){
		if(A[b[2]] + (1 << i) == A[b[1]]){
			B = A;
			flip(B, b[1], b[2], 1 << i);
			dfs(B, i + 1, cnt + 1);
		}
	}
	if(tot == 4){
		vector<int> B;
		if(A[b[1]] + (1 << i) == A[b[3]] && A[b[2]] + (1 << i) == A[b[4]]){
			B = A;
			flip(B, b[2], b[3], 1 << i);
			dfs(B, i + 1, cnt + 1);
		}
		if(A[b[1]] + (1 << i) == A[b[4]] && A[b[3]] + (1 << i) == A[b[2]]){
			B = A;
			flip(B, b[2], b[4], 1 << i);
			dfs(B, i + 1, cnt + 1);
		}
		if(A[b[3]] + (1 << i) == A[b[2]] && A[b[1]] + (1 << i) == A[b[4]]){
			B = A;
			flip(B, b[1], b[3], 1 << i);
			dfs(B, i + 1, cnt + 1);
		}
		if(A[b[4]] + (1 << i) == A[b[2]] && A[b[3]] + (1 << i) == A[b[1]]){
			B = A;
			flip(B, b[1], b[4], 1 << i);
			dfs(B, i + 1, cnt + 1);
		}
	}
}

int main(){
	scanf("%d", &n);
	fact[0] = 1;
	for(int i = 1;i <= n;i ++)
		fact[i] = fact[i - 1] * i;
	a.resize(1 << n);
	for(int i = 0;i < (1 << n);i ++)
		scanf("%d", &a[i]);
	dfs(a, 0, 0);
	printf("%lld\n", ans);
	return 0;
}

【D1T2 寻宝游戏】

不知道大家有没有见过这题啊。。。

把加入的点按dfs序排序，把相邻的两个点以及头尾两个点的距离加起来就是答案了。（证明可以自己脑补）

那么用set维护这些点的位置就好了。

时间复杂度$O((n+m)\log n)$


#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
using namespace std;

#define N 100010

typedef long long ll;

int h[N], g[N], p[N * 2], n1[N * 2], w[N * 2], ee;
int st[N], top, d[N], anc[20][N], n, pos[N], ptot, seq[N], ok[N];
ll dis[N], ans;

set <int> S;
typedef set <int> :: iterator SI;

void ae(int x, int y, int z){
	p[ee] = y; n1[ee] = h[x]; w[ee] = z; h[x] = ee ++;
}

void dfs(){
	memset(d, -1, sizeof(d));
	d[1] = 1;
	pos[1] = ++ ptot;
	seq[1] = 1;
	st[++ top] = 1;
	while(top){
		int u = st[top], flag = 0;
		for(int i = g[u];~i;i = n1[i]){
			if(!~d[p[i]]){
				pos[p[i]] = ++ ptot;
				seq[ptot] = p[i];
				st[++ top] = p[i];
				g[u] = n1[i];
				d[p[i]] = d[u] + 1;
				dis[p[i]] = dis[u] + w[i];
				anc[0][p[i]] = u;
				flag = 1;
				break;
			}
		}
		if(!flag) top --;
	}
}

int lca(int x, int y){
	if(d[x] < d[y]) swap(x, y);
	int k = d[x] - d[y], j = 0;
	while(k){
		if(k & 1) x = anc[j][x];
		k >>= 1;
		j ++;
	}
	if(x == y) return x;
	for(int i = 16;~i;i --) if(anc[i][x] != anc[i][y]) x = anc[i][x], y = anc[i][y];
	return anc[0][x];
}

ll dist(ll x, ll y){
	return dis[x] + dis[y] - 2 * dis[lca(x, y)];
}

int main(){
	int Q;
	scanf("%d%d", &n, &Q);
	memset(h, -1, sizeof(h));
	int x, y, z;
	for(int i = 1;i < n;i ++){
		scanf("%d%d%d", &x, &y, &z);
		ae(x, y, z);
		ae(y, x, z);
	}
	memcpy(g, h, sizeof(h));
	dfs();
	for(int j = 1;j <= 16;j ++)
		for(int i = 1;i <= n;i ++)
			anc[j][i] = anc[j - 1][anc[j - 1][i]];
	SI it, pre, suc;
	while(Q --){
		scanf("%d", &x);
		if(!ok[x]){
			ok[x] = 1;
			pre = suc = it = S.insert(pos[x]).first;
			if(S.size() == 2) ans = 2 * dist(seq[*S.begin()], seq[*S.rbegin()]);
			else if(S.size() > 2){
				if(pre == S.begin()) pre = S.end(), pre --;
				else pre --;
				suc ++;
				if(suc == S.end()) suc = S.begin();
				ans += dist(seq[*pre], x) + dist(seq[*suc], x) - dist(seq[*pre], seq[*suc]);
			}	
		}else{
			ok[x] = 0;
			pre = suc = it = S.find(pos[x]);
			if(S.size() <= 2){
				S.erase(pos[x]);
				ans = 0;	
			}else{
				if(pre == S.begin()) pre = S.end(), pre --;
				else pre --;
				suc ++;
				if(suc == S.end()) suc = S.begin();
				ans -= dist(seq[*pre], x) + dist(seq[*suc], x) - dist(seq[*pre], seq[*suc]);
				S.erase(pos[x]);
			}
		}
		printf("%lld\n", ans);
	}
	return 0;
}

【D1T3 序列统计】

求出$m$的原根$g$，然后对于每个$a_i$求出$g^{b_i}=a_i$。然后问题转化成了在序列$b$中，选出$n$个数（一个数可以取多次），且它们的和$s$满足$s \mod (m - 1) = x$。

用FFT+快速幂可以轻松做到$O(m\log m\log n)$的复杂度。


#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define mo 1004535809
#define ww 3

#define N 300010

int g[20], ng[20], a[N], b[N], c[N], n, len, id[N], K, X, m, G, vis[N], vt, ni;

int pow(int a, int b, int c){
	int ret = 1;
	while(b){
		if(b & 1) ret = 1LL * ret * a % c;
		b >>= 1;
		a = 1LL * a * a % c;
	}
	return ret;
}

void FNT(int *A, int n, int flag){
	for(int i = n >> 1, j = 1;j < n;j ++){
		if(i < j) swap(A[i], A[j]);
		int k;
		for(k = n >> 1;i & k;i ^= k, k >>= 1);
		i ^= k;
	}
	int lg = 0;
	for(int m = 2;m <= n;m <<= 1){
		int w;
		++ lg;
		if(flag == 1) w = g[lg]; else w = ng[lg];
		for(int k = 0;k < n;k += m){
			int cur = 1;
			for(int j = k;j < k + (m >> 1);j ++, cur = 1LL * cur * w % mo){
				int u = A[j], t = 1LL * cur * A[j + (m >> 1)] % mo;
				A[j] = (u + t >= mo) ? (u + t - mo) : (u + t);
				A[j + (m >> 1)] = (u < t) ? (mo + u - t) : (u - t);
			}
		}
	}
}

void FFT_init(){
	for(int i = 1;i < 20;i ++){
		g[i] = pow(ww, (mo - 1) >> i, mo);
		ng[i] = pow(g[i], mo - 2, mo);
	}
}

int check(int k){
	int cur = 1;
	++ vt;
	for(int i = 1;i < n;i ++, cur = cur * k % n){
		if(vis[cur] == vt) return 0;
		vis[cur] = vt;
	}
	return 1;
}

int findroot(){
	for(int i = 2;i <= n;i ++)
		if(check(i)) return i;
}

int main(){
	scanf("%d%d%d%d", &K, &n, &X, &m);
	FFT_init();
	while((1 << len) <= 2 * n) len ++;
	ni = pow(1 << len, mo - 2, mo);
	G = findroot();
	int cur = 1;
	for(int i = 0;i < n - 1;i ++, cur = cur * G % n)
		id[cur] = i;
	int x;
	a[0] = 1;
	for(int i = 1;i <= m;i ++){
		scanf("%d", &x);
                if(x) b[id[x]] ++;
        }
	while(K){
		if(K & 1){
			FNT(a, 1 << len, 1);
			memcpy(c, b, sizeof(b));
			FNT(c, 1 << len, 1);
			for(int i = 0;i < (1 << len);i ++)
				a[i] = 1LL * a[i] * c[i] % mo;
			FNT(a, 1 << len, -1);
			for(int i = 0;i < (1 << len);i ++)
				a[i] = 1LL * a[i] * ni % mo;
			for(int i = n - 1;i < 2 * n - 1;i ++){
				a[i - n + 1] = (a[i - n + 1] + a[i]) % mo;
				a[i] = 0;
			}
		}
		K >>= 1;
		FNT(b, 1 << len, 1);
		for(int i = 0;i < (1 << len);i ++)
			b[i] = 1LL * b[i] * b[i] % mo;
		FNT(b, 1 << len, -1);
		for(int i = 0;i < (1 << len);i ++)
			b[i] = 1LL * b[i] * ni % mo;
		for(int i = n - 1;i < 2 * n - 1;i ++){
			b[i - n + 1] = (b[i - n + 1] + b[i]) % mo;
			b[i] = 0;
		}
	}
	printf("%d\n", a[id[X]]);
	return 0;
}

【D2T1 星际战争】

二分答案，然后弄两排点，能攻击的就连边，求最大流判断是否可行嘛。太裸了吧。


#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;

int h[105], n1[10000], p[10000], ee, d[105], q[105], S, T, a[55], b[55], g[51][51], n, m;
double c[10000], mid;
const double eps = 1e-8;

void ae(int x, int y, double z){
	p[ee] = y; n1[ee] = h[x]; c[ee] = z; h[x] = ee ++;
	p[ee] = x; n1[ee] = h[y]; c[ee] = 0; h[y] = ee ++;
}

int bfs(){
	int s = 1, e = 1;
	memset(d, -1, sizeof(d));
	d[q[1] = S] = 0;
	while(s <= e){
		int u = q[s ++];
		for(int i = h[u];~i;i = n1[i])
			if(c[i] > 0 && !~d[p[i]])
				q[++ e] = p[i], d[p[i]] = d[u] + 1;
	}
	return d[T] != -1;
}

double dfs(int u, double lmt){
	if(u == T) return lmt;
	double ret = 0, del;
	for(int i = h[u];~i;i = n1[i]){
		if(c[i] > 0 && d[p[i]] == d[u] + 1){
			del = dfs(p[i], min(c[i], lmt - ret));
			c[i] -= del;
			c[i ^ 1] += del;
			ret += del;
			if(fabs(ret - lmt) < eps) return ret;
		}
	}
	if(fabs(ret) < eps) d[u] = -1;
	return ret;
}

double dinic(){
	double ret = 0;
	while(bfs()) ret += dfs(S, 1e10);
	return ret;
}

int check(){
	memset(h, -1, sizeof(h));
	ee = 0;
	S = 0;
	T = n + m + 1;
	int sum = 0;
	for(int i = 1;i <= m;i ++)
		ae(S, i, mid * b[i]);
	for(int i = 1;i <= n;i ++)
		ae(m + i, T, a[i]), sum += a[i];
	for(int i = 1;i <= m;i ++)
		for(int j = 1;j <= n;j ++)
			if(g[i][j])
				ae(i, m + j, 1e10);
	return dinic() >= sum;
}

int main(){
	scanf("%d%d", &n, &m);
	for(int i = 1;i <= n;i ++)
		scanf("%d", &a[i]);
	for(int i = 1;i <= m;i ++)
		scanf("%d", &b[i]);
	for(int i = 1;i <= m;i ++)
		for(int j = 1;j <= n;j ++)
			scanf("%d", &g[i][j]);
	double l = 0, r = 5e6;
	while(l + 1e-5 < r){
		mid = (l + r) / 2;
		if(check()) r = mid; else l = mid;
	}
	printf("%.4lf\n", mid);
	return 0;
}

【D2T2 约数个数和】

看到这个应该立马想到CF 235E。。。

[tex]\sum_{i=1}^{n} \sum_{j=1}^{m} d(ij)=\sum_{i=1}^{n} \sum_{j=1}^{m}\lfloor \frac{n}{i} \rfloor \lfloor \frac{m}{j} \rfloor [\gcd(i,j)==1][/tex]

[tex]=\sum_{i=1}^{n}\sum_{j=1}^{m}\lfloor \frac{n}{i} \rfloor \lfloor \frac{m}{j} \rfloor\sum_{k|\gcd(i,j)}\mu(k)[/tex]

[tex]=\sum_{i=1}^{n}\sum_{j=1}^{m}\lfloor \frac{n}{i} \rfloor \lfloor \frac{m}{j} \rfloor\sum_{k|i,k|j}\mu(k)[/tex]

[tex]=\sum_{k}\mu(k)\sum_{i=1}^{\lfloor \frac{n}{k} \rfloor}\sum_{j=1}^{\lfloor \frac{m}{k} \rfloor}\lfloor \frac{n}{ik} \rfloor\lfloor \frac{m}{jk} \rfloor[/tex]

[tex]=\sum_{k}\mu(k)f(\lfloor \frac{n}{k} \rfloor)f(\lfloor \frac{m}{k} \rfloor)[/tex]，其中[tex]f(n)=\sum_{i=1}^{n}\lfloor \frac{n}{i} \rfloor=\sum_{i=1}^{n}d(i)[/tex]

那么我们可以通过线性筛筛出约数个数$d$和$\mu$，询问的时候根号加速。这样整个复杂度就是$O(n+T\sqrt{n})$。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define N 50010

typedef long long ll;
int fl[N], pr[N], miu[N], f[N], g[N], cnt;

void sieve(int n){
	miu[1] = f[1] = 1;
	for(int i = 2;i <= n;i ++){
		if(!fl[i]) pr[++ cnt] = i, miu[i] = -1, f[i] = 2, g[i] = 1;
		for(int j = 1;j <= cnt && i * pr[j] <= n;j ++){
			fl[i * pr[j]] = 1;
			if(i % pr[j] == 0){
				miu[i * pr[j]] = 0;
				g[i * pr[j]] = g[i] + 1;
				f[i * pr[j]] = f[i] / (g[i] + 1) * (g[i] + 2);
				break;
			}
			miu[i * pr[j]] = -miu[i];
			f[i * pr[j]] = f[i] * 2;
			g[i * pr[j]] = 1;
		}
	}
	for(int i = 2;i <= n;i ++)
		f[i] += f[i - 1], miu[i] += miu[i - 1];
}

int main(){
	sieve(N - 10);
	int tc, n, m;
	scanf("%d", &tc);
	while(tc --){
		scanf("%d%d", &n, &m);
		if(n > m) swap(n, m);
		ll ans = 0;
		for(int i = 1, j;i <= n;i = j + 1){
			j = min(n / (n / i), m / (m / i));
			ans += 1LL * (miu[j] - miu[i - 1]) * f[n / i] * f[m / i];
		}
		printf("%lld\n", ans);
	}
	return 0;
}

【D2T3 道路修建】

（听说分治LCT可以写可惜我太弱还没去补过姿势）

[UPD 4.15 听说我这个做法太naive了。被吊打了。。。]

感觉很像BZOJ 1018 堵塞的交通啊。

我们考虑用线段树来维护嘛。

合并的时候，我们就是把两个高度为2的矩形内的东西合并起来。具体的说，我们只要考虑这个矩形四个角的联通情况。我们可以暴力枚举连通状态，然后用最小表示法表示，发现只有10个状态。

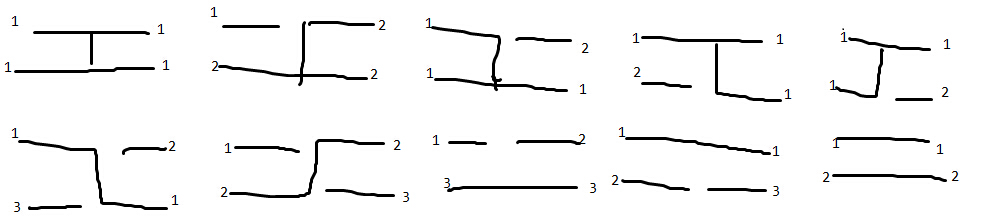
看看上面这图感受一下，标号相同表示他们在一个连通块内。

合并的时候，我们考虑加上两个子区间中间的边，即下图中红色方框的四条边。

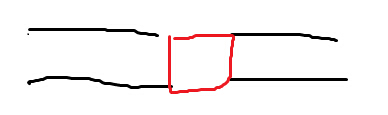
那么我们可以枚举红边的子集，和左右两边的状态，进行暴力合并。每次复杂度10*10*2^4*合并的复杂度……（你TM在逗我笑？）

愉快的发现TLE了。

怎么办？我们可以预处理啊！我们枚举所有的转移状态$(x,y,z,state)$，表示左子树状态$x$和右子树状态$y$加上$state$边集可以合并起来得到状态$z$。然后把这些转移打在表里。发现只有600多种转移！这样复杂度是$O(600n\log n)$。感觉有点虚！

再仔细观察，有的状态是重复的！比如$(x,y)$加上任意3条边，都能转移到$z$。这样我们新建一种转移方式，原来3个转移可以缩减成1个！

经过优化，只剩300个不到个转移了。可以在3S内轻松出解。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 60010
typedef long long ll;
struct node{
	int w[2], cl, cr, f[11];
	void clear(){
		memset(f, 63, sizeof(f));
	}
}t[N << 2];

struct state{
	int x, y, z, s;
}e[300];
#define ls (x << 1)
#define rs (x << 1 | 1)

int W[2][N], C[N], n, Q, num = 266, wsum[18];

void upd(ll &x, ll y){
	x = min(x, y);
}

node merge(node l, node r){
	node x;
	x.w[0] = r.w[0];
	x.w[1] = r.w[1];
	x.cl = l.cl;
	x.cr = r.cr;
	for(int i = 1;i < 15;i ++){
		wsum[i] = 0;
		if(i & 1) wsum[i] += l.w[0];
		if(i & 2) wsum[i] += l.w[1];
		if(i & 4) wsum[i] += l.cr;
		if(i & 8) wsum[i] += r.cl;
	}
	wsum[0] = wsum[14] + l.w[0];
	wsum[16] = l.cr + min(l.w[0], l.w[1]);
	wsum[17] = r.cl + min(l.w[0], l.w[1]);
	x.clear();
	for(int i = 1;i <= num;i ++)
		x.f[e[i].z] = min(x.f[e[i].z], l.f[e[i].x] + r.f[e[i].y] + wsum[e[i].s]);
	return x;
}

void build(int l, int r, int x){
	if(l == r){
		t[x].clear();
		t[x].f[0] = C[l];
		t[x].f[9] = 0;
		t[x].w[0] = W[0][l];
		t[x].w[1] = W[1][l];
		t[x].cl = t[x].cr = C[l];
		return;
	}
	int mid = (l + r) >> 1;
	build(l, mid, ls);
	build(mid + 1, r, rs);
	t[x] = merge(t[ls], t[rs]);
}

node ask(int ql, int qr, int l, int r, int x){
	if(ql <= l && r <= qr) return t[x];
	int mid = (l + r) >> 1;
	if(ql <= mid && mid >= qr) return ask(ql, qr, l, mid, ls);
	if(mid < qr && ql > mid) return ask(ql, qr, mid + 1, r, rs);
	return merge(ask(ql, qr, l, mid, ls), ask(ql, qr, mid + 1, r, rs));
}

void modifyc(int p, int v, int l, int r, int x){
	if(l == r){
		t[x].cl = t[x].cr = v;
		t[x].f[0] = v;
		return;
	}
	int mid = (l + r) >> 1;
	if(p <= mid) modifyc(p, v, l, mid, ls); else modifyc(p, v, mid + 1, r, rs);
	t[x] = merge(t[ls], t[rs]);
}

void modifyw(int p, int v, int vv, int l, int r, int x){
	if(l == r){
		t[x].w[v] = vv;
		return;
	}
	int mid = (l + r) >> 1;
	if(p <= mid) modifyw(p, v, vv, l, mid, ls); else modifyw(p, v, vv, mid + 1, r, rs);
	t[x] = merge(t[ls], t[rs]);
}

void init(){
	e[1] = (state){0, 0, 0, 0}; e[2] = (state){0, 0, 0, 16}; e[3] = (state){0, 0, 0, 17}; e[3] = (state){0, 0, 0, 1}; e[4] = (state){0, 0, 0, 2}; e[5] = (state){0, 0, 0, 3}; e[6] = (state){0, 1, 0, 0}; e[7] = (state){0, 1, 0, 17}; e[7] = (state){0, 1, 0, 3}; e[8] = (state){0, 2, 2, 0}; e[9] = (state){0, 2, 2, 16}; e[10] = (state){0, 2, 2, 17}; e[10] = (state){0, 2, 2, 1}; e[11] = (state){0, 2, 2, 2}; e[12] = (state){0, 2, 2, 3}; e[13] = (state){0, 3, 0, 0}; e[14] = (state){0, 3, 0, 17}; e[14] = (state){0, 3, 0, 3}; e[15] = (state){0, 4, 4, 0}; e[16] = (state){0, 4, 4, 16}; e[17] = (state){0, 4, 4, 17}; e[17] = (state){0, 4, 4, 1}; e[18] = (state){0, 4, 4, 2}; e[19] = (state){0, 4, 4, 3}; e[20] = (state){0, 5, 2, 0}; e[21] = (state){0, 5, 2, 17}; e[21] = (state){0, 5, 2, 3}; e[22] = (state){0, 6, 4, 0}; e[23] = (state){0, 6, 4, 17}; e[23] = (state){0, 6, 4, 3}; e[24] = (state){0, 7, 2, 0}; e[25] = (state){0, 7, 2, 17}; e[25] = (state){0, 7, 2, 3}; e[26] = (state){0, 8, 4, 0}; e[27] = (state){0, 8, 4, 17}; e[27] = (state){0, 8, 4, 3}; e[28] = (state){0, 9, 0, 0}; e[29] = (state){0, 9, 0, 17}; e[29] = (state){0, 9, 4, 1}; e[30] = (state){0, 9, 2, 2}; e[31] = (state){0, 9, 0, 3}; e[32] = (state){0, 9, 4, 5}; e[33] = (state){0, 9, 2, 6}; e[34] = (state){1, 0, 1, 0}; e[35] = (state){1, 0, 1, 16}; e[36] = (state){1, 0, 1, 17}; e[36] = (state){1, 0, 1, 1}; e[37] = (state){1, 0, 1, 2}; e[38] = (state){1, 0, 1, 3}; e[39] = (state){1, 1, 1, 0}; e[40] = (state){1, 1, 1, 17}; e[40] = (state){1, 1, 1, 3}; e[41] = (state){1, 2, 7, 0}; e[42] = (state){1, 2, 7, 16}; e[43] = (state){1, 2, 7, 17}; e[43] = (state){1, 2, 7, 1}; e[44] = (state){1, 2, 7, 2}; e[45] = (state){1, 2, 7, 3}; e[46] = (state){1, 3, 1, 0}; e[47] = (state){1, 3, 1, 17}; e[47] = (state){1, 3, 1, 3}; e[48] = (state){1, 4, 6, 0}; e[49] = (state){1, 4, 6, 16}; e[50] = (state){1, 4, 6, 17}; e[50] = (state){1, 4, 6, 1}; e[51] = (state){1, 4, 6, 2}; e[52] = (state){1, 4, 6, 3}; e[53] = (state){1, 5, 7, 0}; e[54] = (state){1, 5, 7, 17}; e[54] = (state){1, 5, 7, 3}; e[55] = (state){1, 6, 6, 0}; e[56] = (state){1, 6, 6, 17}; e[56] = (state){1, 6, 6, 3}; e[57] = (state){1, 7, 7, 0}; e[58] = (state){1, 7, 7, 17}; e[58] = (state){1, 7, 7, 3}; e[59] = (state){1, 8, 6, 0}; e[60] = (state){1, 8, 6, 17}; e[60] = (state){1, 8, 6, 3}; e[61] = (state){1, 9, 1, 0}; e[62] = (state){1, 9, 1, 17}; e[62] = (state){1, 9, 6, 1}; e[63] = (state){1, 9, 7, 2}; e[64] = (state){1, 9, 1, 3}; e[65] = (state){1, 9, 6, 5}; e[66] = (state){1, 9, 7, 6}; e[67] = (state){2, 0, 0, 0}; e[68] = (state){2, 0, 0, 16}; e[69] = (state){2, 0, 0, 3}; e[70] = (state){2, 1, 0, 0}; e[71] = (state){2, 2, 2, 0}; e[72] = (state){2, 2, 2, 16}; e[73] = (state){2, 2, 2, 3}; e[74] = (state){2, 3, 0, 0}; e[75] = (state){2, 4, 4, 0}; e[76] = (state){2, 4, 4, 16}; e[77] = (state){2, 4, 4, 3}; e[78] = (state){2, 5, 2, 0}; e[79] = (state){2, 6, 4, 0}; e[80] = (state){2, 7, 2, 0}; e[81] = (state){2, 8, 4, 0}; e[82] = (state){2, 9, 0, 0}; e[83] = (state){2, 9, 2, 3}; e[84] = (state){2, 9, 4, 5}; e[85] = (state){2, 9, 2, 6}; e[86] = (state){3, 0, 3, 0}; e[87] = (state){3, 0, 3, 16}; e[88] = (state){3, 0, 3, 17}; e[88] = (state){3, 0, 3, 1}; e[89] = (state){3, 0, 3, 2}; e[90] = (state){3, 0, 3, 3}; e[91] = (state){3, 1, 3, 0}; e[92] = (state){3, 1, 3, 17}; e[92] = (state){3, 1, 3, 3}; e[93] = (state){3, 2, 5, 0}; e[94] = (state){3, 2, 5, 16}; e[95] = (state){3, 2, 5, 17}; e[95] = (state){3, 2, 5, 1}; e[96] = (state){3, 2, 5, 2}; e[97] = (state){3, 2, 5, 3}; e[98] = (state){3, 3, 3, 0}; e[99] = (state){3, 3, 3, 17}; e[99] = (state){3, 3, 3, 3}; e[100] = (state){3, 4, 8, 0}; e[101] = (state){3, 4, 8, 16}; e[102] = (state){3, 4, 8, 17}; e[102] = (state){3, 4, 8, 1}; e[103] = (state){3, 4, 8, 2}; e[104] = (state){3, 4, 8, 3}; e[105] = (state){3, 5, 5, 0}; e[106] = (state){3, 5, 5, 17}; e[106] = (state){3, 5, 5, 3}; e[107] = (state){3, 6, 8, 0}; e[108] = (state){3, 6, 8, 17}; e[108] = (state){3, 6, 8, 3}; e[109] = (state){3, 7, 5, 0}; e[110] = (state){3, 7, 5, 17}; e[110] = (state){3, 7, 5, 3}; e[111] = (state){3, 8, 8, 0}; e[112] = (state){3, 8, 8, 17}; e[112] = (state){3, 8, 8, 3}; e[113] = (state){3, 9, 3, 0}; e[114] = (state){3, 9, 3, 17}; e[114] = (state){3, 9, 8, 1}; e[115] = (state){3, 9, 5, 2}; e[116] = (state){3, 9, 3, 3}; e[117] = (state){3, 9, 8, 5}; e[118] = (state){3, 9, 5, 6}; e[119] = (state){4, 0, 0, 0}; e[120] = (state){4, 0, 0, 16}; e[121] = (state){4, 0, 0, 3}; e[122] = (state){4, 1, 0, 0}; e[123] = (state){4, 2, 2, 0}; e[124] = (state){4, 2, 2, 16}; e[125] = (state){4, 2, 2, 3}; e[126] = (state){4, 3, 0, 0}; e[127] = (state){4, 4, 4, 0}; e[128] = (state){4, 4, 4, 16}; e[129] = (state){4, 4, 4, 3}; e[130] = (state){4, 5, 2, 0}; e[131] = (state){4, 6, 4, 0}; e[132] = (state){4, 7, 2, 0}; e[133] = (state){4, 8, 4, 0}; e[134] = (state){4, 9, 0, 0}; e[135] = (state){4, 9, 4, 3}; e[136] = (state){4, 9, 4, 5}; e[137] = (state){4, 9, 2, 6}; e[138] = (state){5, 0, 3, 0}; e[139] = (state){5, 0, 3, 16}; e[140] = (state){5, 0, 3, 3}; e[141] = (state){5, 1, 3, 0}; e[142] = (state){5, 2, 5, 0}; e[143] = (state){5, 2, 5, 16}; e[144] = (state){5, 2, 5, 3}; e[145] = (state){5, 3, 3, 0}; e[146] = (state){5, 4, 8, 0}; e[147] = (state){5, 4, 8, 16}; e[148] = (state){5, 4, 8, 3}; e[149] = (state){5, 5, 5, 0}; e[150] = (state){5, 6, 8, 0}; e[151] = (state){5, 7, 5, 0}; e[152] = (state){5, 8, 8, 0}; e[153] = (state){5, 9, 3, 0}; e[154] = (state){5, 9, 5, 3}; e[155] = (state){5, 9, 8, 5}; e[156] = (state){5, 9, 5, 6}; e[157] = (state){6, 0, 1, 0}; e[158] = (state){6, 0, 1, 16}; e[159] = (state){6, 0, 1, 3}; e[160] = (state){6, 1, 1, 0}; e[161] = (state){6, 2, 7, 0}; e[162] = (state){6, 2, 7, 16}; e[163] = (state){6, 2, 7, 3}; e[164] = (state){6, 3, 1, 0}; e[165] = (state){6, 4, 6, 0}; e[166] = (state){6, 4, 6, 16}; e[167] = (state){6, 4, 6, 3}; e[168] = (state){6, 5, 7, 0}; e[169] = (state){6, 6, 6, 0}; e[170] = (state){6, 7, 7, 0}; e[171] = (state){6, 8, 6, 0}; e[172] = (state){6, 9, 1, 0}; e[173] = (state){6, 9, 6, 3}; e[174] = (state){6, 9, 6, 5}; e[175] = (state){6, 9, 7, 6}; e[176] = (state){7, 0, 1, 0}; e[177] = (state){7, 0, 1, 16}; e[178] = (state){7, 0, 1, 3}; e[179] = (state){7, 1, 1, 0}; e[180] = (state){7, 2, 7, 0}; e[181] = (state){7, 2, 7, 16}; e[182] = (state){7, 2, 7, 3}; e[183] = (state){7, 3, 1, 0}; e[184] = (state){7, 4, 6, 0}; e[185] = (state){7, 4, 6, 16}; e[186] = (state){7, 4, 6, 3}; e[187] = (state){7, 5, 7, 0}; e[188] = (state){7, 6, 6, 0}; e[189] = (state){7, 7, 7, 0}; e[190] = (state){7, 8, 6, 0}; e[191] = (state){7, 9, 1, 0}; e[192] = (state){7, 9, 7, 3}; e[193] = (state){7, 9, 6, 5}; e[194] = (state){7, 9, 7, 6}; e[195] = (state){8, 0, 3, 0}; e[196] = (state){8, 0, 3, 16}; e[197] = (state){8, 0, 3, 3}; e[198] = (state){8, 1, 3, 0}; e[199] = (state){8, 2, 5, 0}; e[200] = (state){8, 2, 5, 16}; e[201] = (state){8, 2, 5, 3}; e[202] = (state){8, 3, 3, 0}; e[203] = (state){8, 4, 8, 0}; e[204] = (state){8, 4, 8, 16}; e[205] = (state){8, 4, 8, 3}; e[206] = (state){8, 5, 5, 0}; e[207] = (state){8, 6, 8, 0}; e[208] = (state){8, 7, 5, 0}; e[209] = (state){8, 8, 8, 0}; e[210] = (state){8, 9, 3, 0}; e[211] = (state){8, 9, 8, 3}; e[212] = (state){8, 9, 8, 5}; e[213] = (state){8, 9, 5, 6}; e[214] = (state){9, 0, 0, 0}; e[215] = (state){9, 0, 0, 16}; e[216] = (state){9, 0, 3, 1}; e[217] = (state){9, 0, 1, 2}; e[218] = (state){9, 0, 0, 3}; e[219] = (state){9, 0, 3, 9}; e[220] = (state){9, 0, 1, 10}; e[221] = (state){9, 1, 0, 0}; e[222] = (state){9, 1, 1, 3}; e[223] = (state){9, 1, 3, 9}; e[224] = (state){9, 1, 1, 10}; e[225] = (state){9, 2, 2, 0}; e[226] = (state){9, 2, 2, 16}; e[227] = (state){9, 2, 5, 1}; e[228] = (state){9, 2, 7, 2}; e[229] = (state){9, 2, 2, 3}; e[230] = (state){9, 2, 5, 9}; e[231] = (state){9, 2, 7, 10}; e[232] = (state){9, 3, 0, 0}; e[233] = (state){9, 3, 3, 3}; e[234] = (state){9, 3, 3, 9}; e[235] = (state){9, 3, 1, 10}; e[236] = (state){9, 4, 4, 0}; e[237] = (state){9, 4, 4, 16}; e[238] = (state){9, 4, 8, 1}; e[239] = (state){9, 4, 6, 2}; e[240] = (state){9, 4, 4, 3}; e[241] = (state){9, 4, 8, 9}; e[242] = (state){9, 4, 6, 10}; e[243] = (state){9, 5, 2, 0}; e[244] = (state){9, 5, 5, 3}; e[245] = (state){9, 5, 5, 9}; e[246] = (state){9, 5, 7, 10}; e[247] = (state){9, 6, 4, 0}; e[248] = (state){9, 6, 6, 3}; e[249] = (state){9, 6, 8, 9}; e[250] = (state){9, 6, 6, 10}; e[251] = (state){9, 7, 2, 0}; e[252] = (state){9, 7, 7, 3}; e[253] = (state){9, 7, 5, 9}; e[254] = (state){9, 7, 7, 10}; e[255] = (state){9, 8, 4, 0}; e[256] = (state){9, 8, 8, 3}; e[257] = (state){9, 8, 8, 9}; e[258] = (state){9, 8, 6, 10}; e[259] = (state){9, 9, 0, 0}; e[260] = (state){9, 9, 8, 1}; e[261] = (state){9, 9, 7, 2}; e[262] = (state){9, 9, 9, 3}; e[263] = (state){9, 9, 4, 5}; e[264] = (state){9, 9, 2, 6}; e[265] = (state){9, 9, 3, 9}; e[266] = (state){9, 9, 1, 10};
}

int main(){
	scanf("%d%d", &n, &Q);
	for(int j = 0;j < 2;j ++)
		for(int i = 1;i < n;i ++)
			scanf("%d", &W[j][i]);
	for(int i = 1;i <= n;i ++)
		scanf("%d", &C[i]);
	init();
	build(1, n, 1);
	int l, r, x1, y1, x2, y2, ww;
	char op[2];
	while(Q --){
		scanf("%s", op);
		if(op[0] == 'Q'){
			scanf("%d%d", &l, &r);
			printf("%d\n", ask(l, r, 1, n, 1).f[0]);
		}else{
			scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &ww);
			if(y1 == y2) modifyc(y1, ww, 1, n, 1);
			else modifyw(min(y1, y2), x1 - 1, ww, 1, n, 1);
		}
	}
	return 0;
}
  • 无匹配
Small_feed 评论 (1)
1
[回复]
Avatar_small
YZ23 说:
2015年6月11日 19:54

您好，请问D1T3要对卷积的系数取模，如何只用FFT而不用NTT？
谢谢~


登录 *


loading captcha image...
(输入验证码)
or Ctrl+Enter