DZY 's BLOG

先找出基环。

模拟一下发现答案与取球的顺序其实是无关的。

然后去膜拜题解发现的确这样。至于证明蒟蒻看不懂。

但是既然这样就是高精度模拟了？

双倍经验（1416 && 1498）

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
struct Hugeint{int len,num[10000];  Hugeint(){  len=1;  memset(num,0,sizeof(num));}}An1,An2;
int num[1005],A[10000]={0},B[10000]={0},flag[20005]={0},prime[10000],cnt=0,sum=0;
inline int pre(int n){
    for(int i=2;i<=n;i++){
        if(!flag[i]) prime[cnt++]=i;
        for(int j=0;j<cnt&&prime[j]*i<=n;j++){
            flag[i*prime[j]]=1;
            if(i%prime[j]==0)break;
        }
    }
}inline Hugeint Mul(Hugeint a,Hugeint b){
    Hugeint c;  c.len=a.len+b.len+1;
    for(int i=1;i<=a.len;i++) for(int j=1;j<=b.len;j++)  c.num[i+j-1]+=a.num[i]*b.num[j];
    for(int i=1;i<c.len;i++)  if(c.num[i]>9999) c.num[i+1]+=c.num[i]/10000,c.num[i]%=10000;
    while(c.num[c.len]>9999) c.len++,c.num[c.len]+=c.num[c.len-1]/10000,c.num[c.len-1]%=10000;
    while(c.num[c.len]==0&&c.len>1) c.len--;   return c;
}inline Hugeint pow(int b,int p){
    Hugeint ans,bb; ans.len=bb.len=ans.num[1]=1ll;  bb.num[1]=b;
    while(p){if(p&1ll)ans=Mul(ans,bb);p>>=1ll;bb=Mul(bb,bb);}   return ans;
}void print(Hugeint a){
    printf("%d",a.num[a.len]); for(int i=a.len-1;i;i--)printf("%04d",a.num[i]);
}inline void pushA(int k){
    for(int i=0;k>1&&i<cnt&&prime[i]<=k;i++) while(k%prime[i]==0)A[i]++,k/=prime[i];
}inline void pushB(int k){
    for(int i=0;k>1&&i<cnt&&prime[i]<=k;i++) while(k%prime[i]==0)B[i]++,k/=prime[i];
}int main(){
    int n,m,d,x,y;  pre(20000);
    scanf("%d%d%d",&n,&m,&d); for(int i=1;i<=n;i++)scanf("%d",&num[i]),sum+=num[i];
    for(int i=1;i<=m;i++){
        scanf("%d%d",&x,&y);
        if(num[y]==0){ printf("0/1\n");return 0;}
        pushA(num[y]);  pushB(sum);
        num[y]+=d;      sum+=d;
    }for(int i=0;i<cnt;i++) if(A[i]&&B[i]){
        if(A[i]>B[i])   A[i]-=B[i], B[i]=0;
        else            B[i]-=A[i], A[i]=0;
    }An1.num[1]=An2.num[1]=1;
    for(int i=0;i<cnt;i++)  if(A[i])    An1=Mul(An1,pow(prime[i],A[i]));
    for(int i=0;i<cnt;i++)  if(B[i])    An2=Mul(An2,pow(prime[i],B[i]));
    print(An1);putchar('/');print(An2);putchar('\n');return 0;
}

开始题目什么意思都没看懂。后来明白了是求一些圆和等腰梯形的面积并。

先根据样例画个图。明确算的是哪一部分。

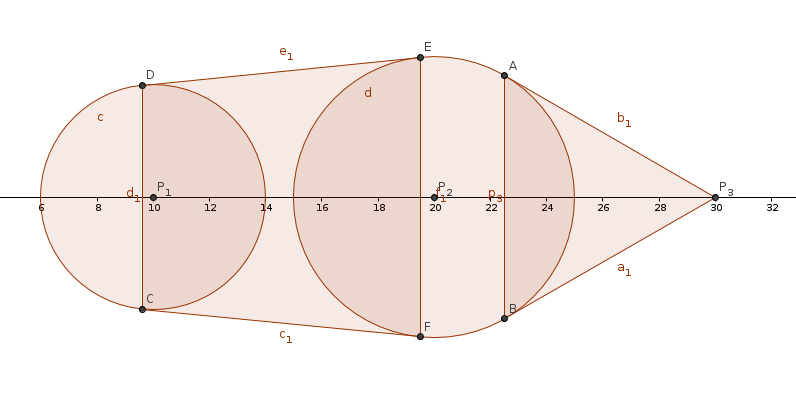
最后要求的就是这些图形的面积并了。怎么求呢？需要用到simpson积分公式。由于我太弱所以就讲的意识流一些。或许不是那么严谨吧。

首先要预处理出这些等腰梯形。他们是由相邻两圆的公切线（如果不存在就不用算了）和两条过切点垂直于x轴的线段组成的。这4个点可以通过相似算出。

重点：simpson(l,r)=(f(l)+4f(mid)+f(r))*(r-l)/6. 其中f(x)当然是一个分段函数.每次O(n)可以算出（枚举所有的等腰梯形和圆）

对于定义在[l,r]上的连续函数，求它和x轴、直线x=l、直线x=r围成的面积S=rsimpson(l,r)。当simpson(l,r)=simpson(l,mid)+simpson(mid,r)时，返回simpson(l,r)；否则返回rsimpson(l,mid)+rsimpson(mid,r)。显然，答案就是2*simpson(l,r)。

【拓展】

辛普森的简化公式可以用来算体积V：V=h(a+4b+c)/6。

h是立体（常指拟柱体）的高度，a是下底面积，b是中间截面面积（在一半高度上的截面面积），c是上底面积。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const double eps=1e-6;
double x[505],r[505],sx[505],sy[505],tx[505],ty[505],L,R,af,t=0;int n;
double f(double xx){
    double fx=0;
    for(int i=1;i<=n+1;i++) if(fabs(xx-x[i])<=r[i]) fx=max(fx,sqrt(r[i]*r[i]-(xx-x[i])*(xx-x[i])));
    for(int i=1;i<=n;i++)   if(x[i+1]-x[i]-fabs(r[i+1]-r[i])>eps && sx[i]<=xx && xx<=tx[i]){
        if(sy[i]<ty[i]) fx=max(fx,sy[i]+(ty[i]-sy[i])*(xx-sx[i])/(tx[i]-sx[i]));
        else            fx=max(fx,ty[i]+(sy[i]-ty[i])*(tx[i]-xx)/(tx[i]-sx[i]));
	}return fx;
}double simpson(double l,double r){
    return (f(l)+f(r)+4*f((l+r)/2.0))*(r-l)/6.0;
}double rsimpson(double l,double r){
    double mid=(l+r)/2.0;
    if(fabs(simpson(l,r)-simpson(l,mid)-simpson(mid,r))<eps)	return simpson(l,mid)+simpson(mid,r);
    return rsimpson(l,mid)+rsimpson(mid,r);
}int main(){
    scanf("%d%lf",&n,&af);  af=1.0/tan(af);
    for(int i=1;i<=n+1;i++) scanf("%lf",&x[i]),t+=x[i],x[i]=t*af;
    for(int i=1;i<=n;i++)   scanf("%lf",&r[i]);L=x[1],R=x[n+1],r[n+1]=0;
    for(int i=1;i<=n;i++){
        L=min(L,x[i]-r[i]), R=max(R,x[i]+r[i]);
        if(x[i+1]-x[i]-fabs(r[i+1]-r[i])>eps){
            double o=(r[i+1]-r[i])/(x[i+1]-x[i]);
            sx[i]=x[i]-r[i]*o,  sy[i]=sqrt(r[i]*r[i]*(1-o*o));
            tx[i]=x[i+1]-r[i+1]*o,  ty[i]=sqrt(r[i+1]*r[i+1]*(1-o*o));
        }
    }printf("%.2lf\n",2*rsimpson(L,R));	return 0;
}