DZY 's BLOG
Hello World!
PA 2011 Solution
[1.2]final的题终于切完了,只差一道[A]组题了!(题目好像太脑洞了,求做法,不然好像只能抽空膜拜代码了)
现在的进度:
| OK 96% |
24
[12.26]继续开新坑- -
[12.27]上两位数了,有点感人。(你也不看看几道水题?)
[12.28]过半了,有点感人。(就多了几道题?)
[12.29]完成18/25了,有点感人。(这个数字有什么意义吗?)
[12.30]2开头了,好感人。
[12.31]还差3题...唉要拖到明年了..T.T
[1.1]现在Round和Final还各差一题,感觉要熬出头了。
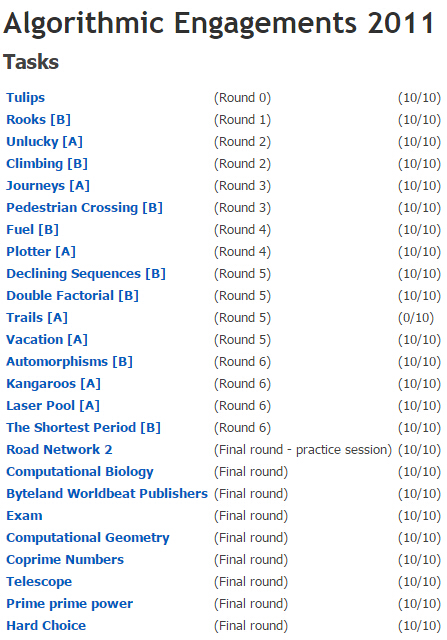
| Tulips | (Round 0) | (10/10) |
考你会不会编程 = =
| Rooks [B] | (Round 1) | (10/10) |
贪心放即可。
| Unlucky [A] | (Round 2) | (10/10) |
怎么会有这么丧病的题。。。设总长度为[tex]S[/tex],总水量为[tex]N[/tex],背包容量为[tex]K[/tex]。方便起见我们先考虑[tex]N[/tex]是[tex]K[/tex]的倍数的情况。显然一个贪心的策略就是每次我们每次都是装满背包出发的,尽量的利用之前带出的水使右端点一点点右移,到终点。可是策略是什么呢= =想了半天也想不出来,于是找了个程序膜拜了一下。大致看懂了。
先解释下样例。
(1)带10的水出来到2,放下6升,回去。
(2)带10的水出来到2,补2升,满了。然后走到5.3333。还剩6.66666。放下3.3333。走回2,一滴水都没了。补2升。走回起点。
(3)带10的水到2,补2升,满了。走到5.3333。还剩6.6666。拿上上次放的3.333,又满了。走到终点,还剩10-(10-5.333)=5.3333
显然你可以出发[tex]C=\frac{N}{K}[/tex]次,假设你现在还要走[tex]C[/tex]次,那么你接下来会有[tex]2C-1[/tex]次要经过这里。(除了最后一次直接去终点以外都是过去还要回终点的)。那我们把这K均分成[tex]2C-1[/tex]份即可。这样每次右移的距离就是[tex]\frac{K}{2\times C'-1}[/tex]。如果可以直接走到终点了,那我们就先直接走到终点。剩下的次数用来把最靠右边的水都拿回来。
如果[tex]K[/tex]不是整除[tex]N[/tex]的,那就把多出来的那部分先考虑,方法相同。
| Climbing [B] | (Round 2) | (10/10) |
我们假设每一对的右边那个球的可行高度为[tex][L,R][/tex],然后就能列出不等式了。贪心的一段一段放,如果不可行了就新开一段。
| Journeys [A] | (Round 3) | (10/10) |
用线段树处理一下一个线段能到达的所有线段。用vector维护下。然后实现一个bfs的过程即可。用set把还未更新的点都抓出来,然后在线段树上找到新的区间插入队列即可。STL大法好!
| Pedestrian Crossing [B] | (Round 3) | (10/10) |
假设就从起点出发。因为步长确定的,所以我们一切计算都在模步长的意义下做就行了。对于每个白块处理一下距离起点的长度范围 满足 从这个范围出发会和这个白块相交。然后看看所有区间是不是覆盖了[0,步长),如果完全覆盖就不合法了。
| Fuel [B] | (Round 4) | (10/10) |
贪心。走最长链一定最优。剩下的点都是最长链的分支,可以发现走一个的代价均为2。没了。
| Plotter [A] | (Round 4) | (10/10) |
[tex]l_1=L[/tex]
[tex]l_n=l_{n-1}Lf(l_{n-1})[/tex]
[tex]f(l)[/tex]表示把串[tex]l[/tex]反转,然后把L改成R,R改成L。
从画出的图像可以看出[tex]l_n[/tex]由[tex]l_{n-1}[/tex]和它顺时针旋转90°后的图案组成的。
所以我们每次可以把问题递归到两边。显然[tex]n[/tex]大概60多的时候就没用了,坐标已经过大了。显然要加个剪枝,就是处理出[tex]l_n[/tex]的最小包裹的矩形的范围,超过这个范围就不用搜下去了。
| Declining Sequences [B] | (Round 5) | (10/10) |
先用树状数组处理一下每个点开始长度为[tex]l[/tex]的下降序列有几个。然后找第[tex]k[/tex]小的话显然是利用预处理的那个东西找就行了。暴力一次[tex]\text{O}(n)[/tex]嘛,然后可以离线然后用线段树在[tex]\text{O}(\text{log}n)[/tex]的时间完成找下一位的操作。
| Double Factorial [B] | (Round 5) | (10/10) |
显然就是问答案里有几个质因子5。一个显然的式子用高精度算一下即可。
| Vacation [A] | (Round 5) | (10/10) |
n只有5000,猜匹配可以过。每个点只跟自己附近的15个点连边就好了。费用流T了。。换成KM就过了。。真可怕。。
| Automorphisms [B] | (Round 6) | (10/10) |
计算树的同构数。用hash计算子树的形状。假设对于一颗有根树,[tex]s[/tex]这个状态的子树有[tex]f[s][/tex]种同构数,这个状态出现了[tex]cnt[s][/tex]次,那么显然答案为\(\prod_{s\in Son}f[s]^{cnt[s]}cnt[s]!\)。这一步的hash函数好像要强一点...不然会WA...最后我是把子树大小和节点度数都加进去了。
因为这个时候我们假设1是映射到它自己的。那么我们还需计算一下有多少个点作为根的时候树的形态不变。设计一个类似+-或者xor的hash可以方便解决。
| Kangaroos [A] | (Round 6) | (10/10) |
两个区间如果有交集,那就是[tex]L\leq R',R \geq L'[/tex]。考虑分块,如果答案横跨多个块的,我们维护前缀和后缀的[tex]L_{max},R_{min}[/tex]然后二分,最后扫一遍全部的块。否则块内对于每个长度[tex]i(1\leq i \leq size)[/tex],我们把所有这个长度的连续段的[tex]L_{max},R_{min}[/tex]处理出来,然后剔除无效的状态,满足两端都有单调性,就可以二分答案之后再二分判断了。于是询问复杂度是[tex]\text{O}(\frac{NQ}{L}\text{log}^2 L)[/tex]的样子,取[tex]L=\sqrt{N \text{log}N}[/tex]附近配合fread就能过了= =
| Laser Pool [A] | (Round 6) | (10/10) |
终于A了这代码题。。
显然我们要计算每条斜线上有几个横线和竖线的交点即可。完整的线可以用FFT与预处理。
然后剩下来两端多出来的可以用bitset大法。
接下来就是分类讨论时间!
有几个可以变得方便的小细节。比如可以把中间[tex]n-2[/tex]条线向上翻上去,中间[tex]m-2[/tex]条线向右翻过去,这样只用处理[tex]v_x=1,v_y=-1[/tex]的情况,要方便许多。
剩下的就是时间的问题了>.<
| The Shortest Period [B] | (Round 6) | (10/10) |
挺不错的字符串题。ZJOI2013上Seter有讲过。
假设删掉一个字符后,我们得到了[tex]S'[/tex]。如果[tex]S'[/tex]有一个长度为[tex]x[/tex]的循环节,那把[tex]S'[/tex]翻转过来它显然也有一个长度为[tex]x[/tex]的循环节。
如:[tex]S'=abaabaab[/tex],正的时候循环节是[tex]aba[/tex],倒过来循环节就是[tex]baa[/tex],长度都为3。
我们先枚举答案[tex]L[/tex]。
如:[tex]S[1..n]=ababdaba[/tex]。我们先计算一次[tex]S[1][/tex]和[tex]S[L + 1][/tex]的LCP,找出第一个失配字符。然后忽略这个字符再在后面的串中做一次LCP,判断是否可行即可。
正的和逆的都做一遍。
上述情况是我们假设这个失配字符不在前[tex]L[/tex]或后[tex]L[/tex]个字符中,因为这样我们实际上是确定了循环节。因此还有一种情况就是失配字符两边都出现了。
那我们只需比较[tex]S[1..L][/tex]和[tex]S[n - L + 1..n][/tex]是否匹配即可,因为中间的失配字符出现的位置不影响答案。
最后实现可以用hash简单快速...倍增在MAIN上T了,DC3也跑不过hash...好伤人> <
| Road Network 2 | (Final round - practice session) | (10/10) |
度数和似乎得是[tex]2n-2[/tex]才有解。于是判度数和的时候他好像会故意给你爆int = = 真丧病。然后度数从小到大排序,每次拿前面的即可,注意留出一个度数给它的父亲。当然最后根要拿完。
| Computational Biology | (Final round) | (10/10) |
把所有长度为[tex]m[/tex]的串做hash。然后把每个串的第一个字符提出来放到最后,再算一次hash。然后这两个字符串的hash连有向边。这样满足题意的串一定形成一个环。每个点的点权就是出现次数了。然后就是dfs找最大环了。dfs要线性(不要用map= =)不然会T。
| Byteland Worldbeat Publishers | (Final round) | (10/10) |
Orz JC!!
首先会想到求出最小匹配和最大匹配?再一想要是能求出来那简直神作了。
小细节是[tex]n,m[/tex]如果不等就都赋为较大值即可。
大概就是如果有一个匹配,其中有[tex]x_1[/tex]配[tex]y_1[/tex],[tex]x_2[/tex]配[tex]y_2[/tex]。然后[tex]w(x_1,y_1)+w(x_2,y_2)\not= w(x_1,y_2)+w(x_2,y_1)[/tex]那交换一下这两对答案就会发生变化了。于是我们发现如果答案始终不会变,那一定有[tex]w(x_1,y_1)+w(x_2,y_2)= w(x_1,y_2)+w(x_2,y_1)[/tex],变形成[tex]w(x_1,y_1)-w(x_2,y_1)=w(x_1,y_2)-w(x_2,y_2)[/tex],由此看出[tex]w(x1,y)-w(x2,y)[/tex]应该是个常数。设其为[tex]d(x1,x2)[/tex],我们给左边的点都标号[tex]a_i[/tex],然后设[tex]d(x1,x2)=a_{x_1}-a_{x_2}[/tex]。由定义得这东西有传递性,那么设[tex]a_1=0[/tex],就可以处理出[tex]a_i[/tex]了。然后同理给右边的点标号[tex]b_i[/tex],在合法的情况下标号显然都要满足[tex]a_i+b_j=w(i,j)[/tex]。我们可以全部取1为特殊点,然后处理出所有标号。然后枚举左边的点,对每一段区间检验上述等式是否成立。查询最大最小值是否相同即可。复杂度为[tex]\text{O}(n\text{log} n+m)[/tex]。
| Exam | (Final round) | (10/10) |
因为边长已经固定了,那么计算答案的时候只用考虑左下角端点的贡献即可。转化为插入一个点,询问一个矩形内是否有点。离线CDQ分治即可,拆成4个点,用个bit维护一下矩形内点的数量。复杂度两个log。
| Computational Geometry | (Final round) | (10/10) |
好弱的构造题。可以通过多边形内角和算出拐90°弯的次数是[tex]\frac{n}{2}+2[/tex],可见奇数无解。那么构造的时候就是一高一低的样子即可。低的全放1,高的平均分即可。
| Coprime Numbers | (Final round) | (10/10) |
容斥。[tex]f[i][/tex]表示以[tex]i[/tex]为公约数的有序对数。要预处理一下有多少个[tex]a_i[/tex]是[tex]k[/tex]的倍数之类的东西,暴力枚举即可,复杂度[tex]\text{O}(a_i\text{log}a_i)[/tex]
| Telescope | (Final round) | (10/10) |
一眼就是dp题,但是范围太大不好离散化。Orz JC发现最优解的结构一定是若干段。然后每一段里面,每个区间距离都是[tex]r[/tex],且最后一个区间的左端点覆盖在点上。
有了这个发现之后就很好做了。先预处理出[tex]f[i][j][s][/tex]表示第i个点作为第j个区间的左端点,然后使用了[tex]s[/tex]状态的区间,能覆盖的最多的点。有了[tex]i,j,s[/tex]之后,就能处理出一个区间[tex][l,r][/tex],其状态为[tex]s[/tex],收益为[tex]w=f[i][j][s][/tex]。然后就是让你求不相交的线段,且线段的状态交集为0,最大化收益和。我们发现右端点其实只有[tex]nm[/tex]个,然后对它们离散化。然后就是简单的树状数组求最大值。复杂度大概是[tex]\text{O}(nm^2 2^m+nm3^m\text{log}(nm))[/tex]。(好差的复杂度但是还能A= =)
| Prime prime power | (Final round) | (10/10) |
容易发现指数只能在61以下,只有18个质数。然后确定底数的范围即可。初始范围可以用对数,然后暴力检查。然后每次从堆里取最小的然后调整。中间过程涉及到找大于[tex]x[/tex]的最小质数。暴力枚举然后miller-rabbin判断。(只有幂为2的时候才会涉及到大质数,于是可以预处理一些这个范围内的合数,减少miller-rabbin的操作次数,可以减少很多时间)然后就是卡常数了233 MAIN上0.8s一个点本地开O2一定要跑进0.1s不然TLE。。蛤蛤。。最后终于把参数调科学了。。。
| Hard Choice | (Final round) | (10/10) |
一张图,每次可以删一条边,询问两个点之间是否至少有两条不同的路径。两条路径是不同的,当且仅当他们没有公共边,可以有公共点。
显然转化为求两个点在不在一个边双里,然后把询问倒过来,变成加边操作。
这个也可以用LCT维护。合并的时候把一条路径取出来缩成一个BCC。具体实现就是把LCT里的虚父亲设为BCC里的父亲,然后把路径上的点全部暴力在并查集中和根合并,这样BCC就缩在根上了,最后把根节点提出来就好了。Orz JC
然后发现有两个点T的很惨烈。。。。原来是单旋spaly被卡掉辣蛤蛤蛤。。。出题人我们还能不能愉快玩耍。。。。改成双旋之后快了50倍你敢信?。。淦!
- 无匹配
2014年12月29日 09:29
跪PA爷!
2014年12月29日 11:18
@jiry_2: 被D了!
2015年1月01日 19:48
=w=好棒
2015年1月02日 17:21
唉我现在连B组题都各种不会做。。感觉人生失去了希望。。T^T
2015年1月03日 00:45
@jiry_2: 太假。。。T T
2023年1月19日 18:54
The PA 2011 solution is a comprehensive, collaborative effort to reduce the Pennsylvania government’s budget deficit. The solution included a number of different measures, including CBD Edibles a hiring freeze, spending cuts, and revenue increases. The solution was the result of a months-long effort by a bipartisan group of state lawmakers and officials.