DZY 's BLOG

数据范围≤30、、哈哈这么小啊、、

给你一个n*m的点阵、有些点是障碍、求一个欧几里得距离最大的点对(A,B)，使得在移走的障碍≤T的情况下，可以从A走到B、

由于数据范围小的出奇那么可以大胆考虑对每个点做一次spfa、连边这样连：(u,v)如果v是障碍那么连的边权就是1、否则连0、每个点都向上下左右各连一条边、接下来跑spfa、要注意一点：如果以一个障碍点为源点开始spfa、那么t要先减一、因为首先得把这个位置上的障碍移掉、然后跑出来每个点的距离就是要移开的障碍数、小于等于T就更新答案即可、

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
#define pos(x,y) (((x)-1)*m+(y))
int p[10000],w[10000],n1[10000],h[1000],d[1000],q[500000],v[1000],a[40][40],tot=0,n,m,t,An=0;
char s[40]; int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
inline void ae(int a,int b,int c){
    p[tot]=b;   w[tot]=c;   n1[tot]=h[a];  h[a]=tot++;
}inline void spfa(int S){
    memset(d,63,sizeof(d)); memset(v,0,sizeof(v));
    int head=0,tail=1;  q[0]=S; v[S]=1; d[S]=0;
    while(head<tail){
        int u=q[head++];    v[u]=0;
        for(int i=h[u];~i;i=n1[i]){
            if(d[p[i]]>d[u]+w[i]){
                d[p[i]]=d[u]+w[i];
                if(!v[p[i]])    q[tail++]=p[i], v[p[i]]=1;
            }
        }
    }
}inline void build(){
    memset(h,0xff,sizeof(h));
    for(int i=1;i<=n;i++)   for(int j=1;j<=m;j++){
        for(int k=0;k<4;k++){
            int xx=i+dx[k],yy=j+dy[k];
            if(xx>=1&&xx<=n&&yy>=1&&yy<=m)  ae(pos(i,j),pos(xx,yy),a[xx][yy]);
        }
    }
}int main(){
    scanf("%d%d%d",&n,&m,&t);
    for(int i=1;i<=n;i++){
        scanf("%s",s+1);
        for(int j=1;j<=m;j++)   a[i][j]=s[j]-'0';
    }build();
    for(int i=1;i<=n;i++)   for(int j=1;j<=m;j++){
        spfa(pos(i,j)); t-=a[i][j];
        for(int u=1;u<=n;u++)   for(int v=1;v<=m;v++)
            if(d[pos(u,v)]<=t)  An=max(An,(u-i)*(u-i)+(v-j)*(v-j));
        t+=a[i][j];
    }printf("%.6lf\n",sqrt((double)An));
    return 0;
}

n个顶点的有向图，每条边的边权都在1~9。问从1到n的长度为t的路径有几条。

看时间10^9立即想到矩乘。而且n≤10，边权范围只有9。那么把每个点都拆成9个。构造01矩阵。

一个点拆成9个之后这9个点首先要连通。然后就是(u,v,w)的边，从(u,w)连一条边到(v,1)，最后答案就是Matrix[1][(n,1)]。

复杂度：O(81*n^3*log(t))。rank5、、呵呵、、还不慢、、

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define pos(x,y) (9*((x)-1)+y)
struct matrix{
    int r,c,num[95][95];
    matrix(){memset(num,0,sizeof(num));};
    matrix(int _r,int _c):r(_r),c(_c){memset(num,0,sizeof(num));};
    inline void setone(){   for(int i=1;i<=r;i++)   num[i][i]=1;}
    matrix operator * (matrix b)const{
        matrix d(r,b.c);    for(int i=1;i<=r;i++)   for(int j=1;j<=b.c;j++){
            for(int k=1;k<=c;k++)   d.num[i][j]+=num[i][k]*b.num[k][j];
            d.num[i][j]%=2009;
        }return d;
    }
}A; int n,t;    char s[12];
matrix operator ^(matrix a,int b){
    matrix d(a.r,a.c);  d.setone();
    while(b){   if(b&1) d=d*a;  b>>=1;  a=a*a;} return d;
}int main(){
    scanf("%d%d",&n,&t);    A.r=A.c=9*n;
    for(int i=1;i<=n;i++)   for(int j=1;j<=8;j++)   A.num[pos(i,j)][pos(i,j+1)]=1;
    for(int i=1;i<=n;i++){
        scanf("%s",s+1);
        for(int j=1;j<=n;j++)   if(s[j]-'0')    A.num[pos(i,s[j]-'0')][pos(j,1)]=1;
    }printf("%d\n",(A^t).num[1][pos(n,1)]);
    return 0;
}

一直想做一道跟礼物有关的题、于是做了这道、

题意：长度为2^31的数轴上有n(<100w)个不同颜色的点，颜色种类<60，求一个长度最短的区间包含所有颜色的点。

思路好像很快就有了。记录每种颜色出现的第一个点和下一个点、把每种颜色的第一个点放进堆。这算一个初始答案。

之后每次把最左端的点从堆中删除、插入下一个这种颜色的点、直到删除的点没有后继了、那么答案也不能继续更新了（这不是废话？

那么就好了、我比较偷懒就用了priority_queue、、嘿嘿、、、（重载运算符真坑、、被坑了好久、、

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int inf=1000000009;
int d[1000005],h[65],p[1000005],tot=0,L=inf,R=-1,An=inf;
typedef struct gift{
    int x,y;
    gift(){}
    gift(int _x,int _y):x(_x),y(_y){}
    inline bool operator < (gift b)const{
        if(d[x]==d[b.x]){
            if(y==-1)   return 0;   if(b.y==-1) return 1;
            return d[y]>d[b.y];
        }return d[x]>d[b.x];
    }
};
priority_queue<gift>Q;
inline void read(int &x){
    char ch;    for(ch=getchar();ch<'0'||ch>'9';ch=getchar());
    x=ch-'0';   for(ch=getchar();ch>='0'&&ch<='9';ch=getchar())x=x*10+ch-'0';
}int main(){
    int n,k,t,x;    read(n);    read(k);    memset(p,0xff,sizeof(p));
    while(!Q.empty())   Q.pop();
    for(int i=1;i<=k;i++){
        read(t);    read(d[h[i]=tot++]);
        for(int x=h[i],j=2;j<=t;j++,x=p[x])    p[x]=tot++, read(d[p[x]]);
        Q.push(gift(h[i],p[h[i]]));   L=min(L,d[h[i]]),    R=max(R,d[h[i]]);
    }An=R-L;
    while(Q.top().y!=-1){
        gift u=Q.top();    Q.pop();
        if(d[u.y]>R)   R=d[u.y];  Q.push(gift(u.y,p[u.y]));
        if(R-d[Q.top().x]<An)    An=R-d[Q.top().x];
    }printf("%d\n",An);
    return 0;
}

开始题目什么意思都没看懂。后来明白了是求一些圆和等腰梯形的面积并。

先根据样例画个图。明确算的是哪一部分。

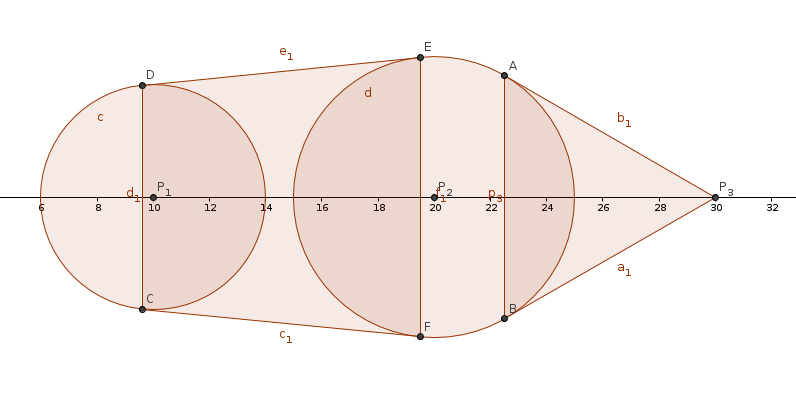
最后要求的就是这些图形的面积并了。怎么求呢？需要用到simpson积分公式。由于我太弱所以就讲的意识流一些。或许不是那么严谨吧。

首先要预处理出这些等腰梯形。他们是由相邻两圆的公切线（如果不存在就不用算了）和两条过切点垂直于x轴的线段组成的。这4个点可以通过相似算出。

重点：simpson(l,r)=(f(l)+4f(mid)+f(r))*(r-l)/6. 其中f(x)当然是一个分段函数.每次O(n)可以算出（枚举所有的等腰梯形和圆）

对于定义在[l,r]上的连续函数，求它和x轴、直线x=l、直线x=r围成的面积S=rsimpson(l,r)。当simpson(l,r)=simpson(l,mid)+simpson(mid,r)时，返回simpson(l,r)；否则返回rsimpson(l,mid)+rsimpson(mid,r)。显然，答案就是2*simpson(l,r)。

【拓展】

辛普森的简化公式可以用来算体积V：V=h(a+4b+c)/6。

h是立体（常指拟柱体）的高度，a是下底面积，b是中间截面面积（在一半高度上的截面面积），c是上底面积。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const double eps=1e-6;
double x[505],r[505],sx[505],sy[505],tx[505],ty[505],L,R,af,t=0;int n;
double f(double xx){
    double fx=0;
    for(int i=1;i<=n+1;i++) if(fabs(xx-x[i])<=r[i]) fx=max(fx,sqrt(r[i]*r[i]-(xx-x[i])*(xx-x[i])));
    for(int i=1;i<=n;i++)   if(x[i+1]-x[i]-fabs(r[i+1]-r[i])>eps && sx[i]<=xx && xx<=tx[i]){
        if(sy[i]<ty[i]) fx=max(fx,sy[i]+(ty[i]-sy[i])*(xx-sx[i])/(tx[i]-sx[i]));
        else            fx=max(fx,ty[i]+(sy[i]-ty[i])*(tx[i]-xx)/(tx[i]-sx[i]));
	}return fx;
}double simpson(double l,double r){
    return (f(l)+f(r)+4*f((l+r)/2.0))*(r-l)/6.0;
}double rsimpson(double l,double r){
    double mid=(l+r)/2.0;
    if(fabs(simpson(l,r)-simpson(l,mid)-simpson(mid,r))<eps)	return simpson(l,mid)+simpson(mid,r);
    return rsimpson(l,mid)+rsimpson(mid,r);
}int main(){
    scanf("%d%lf",&n,&af);  af=1.0/tan(af);
    for(int i=1;i<=n+1;i++) scanf("%lf",&x[i]),t+=x[i],x[i]=t*af;
    for(int i=1;i<=n;i++)   scanf("%lf",&r[i]);L=x[1],R=x[n+1],r[n+1]=0;
    for(int i=1;i<=n;i++){
        L=min(L,x[i]-r[i]), R=max(R,x[i]+r[i]);
        if(x[i+1]-x[i]-fabs(r[i+1]-r[i])>eps){
            double o=(r[i+1]-r[i])/(x[i+1]-x[i]);
            sx[i]=x[i]-r[i]*o,  sy[i]=sqrt(r[i]*r[i]*(1-o*o));
            tx[i]=x[i+1]-r[i+1]*o,  ty[i]=sqrt(r[i+1]*r[i+1]*(1-o*o));
        }
    }printf("%.2lf\n",2*rsimpson(L,R));	return 0;
}